|
Combinatorial Equilibrium Modelling: A computational framework for equilibrium-based structural design |
P.O. Ohlbrock 2014 - 2020 |

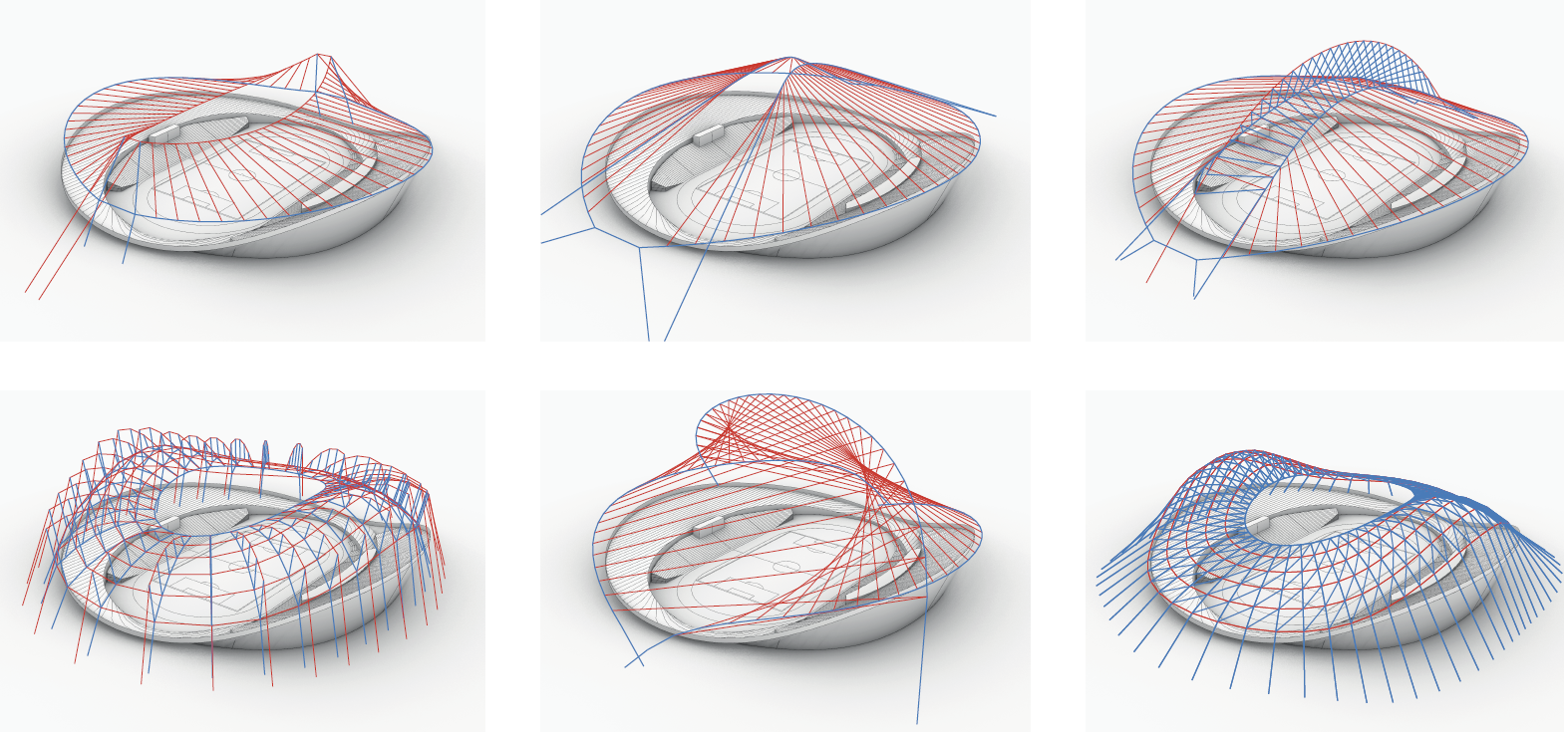
This dissertation presents the Combinatorial Equilibrium Modelling (CEM), a new structural design framework for the early conceptual design phase at the interface between architecture and engineering. The developed framework supports the interactive generation, evaluation and transformation of unconventional mixed (compression-tension) equilibrium models beyond funicular systems. Grounded on the lower bound theorem of the theory of plasticity, the proposed framework is focused on the diagrammatic visualization of equilibrium states. These diagrammatic models are helpful to enhance the dialogue between essential architectural and structural aspects in the early design phase, in both a solution-oriented (explorative) mode, and in the problem-oriented (convergent) mode. In the explorative design phase, designers usually search for satisfying solutions by alternately generating and evaluating design proposals, rather than trying to understand the nature of the ill-defined design problem. One can argue generating radically different proposals in this early design stage would help to obtain a clearer picture of the essential features of the design problem. In the field of structural design, however, only a limited number of proposals that are directly derived from a catalogue of well-known structural typologies are commonly considered. In this regard, this dissertation promotes an alternative strategy, which is characterized by going back to fundamental principles and originating design proposals through combining basic structural considerations. At the core of the proposed CEM framework, the CEM algorithm is able to generate at speed equilibrium models for any given combination of compression and tension edges and the applied loads. The CEM algorithm is based on a sequential partitioning and consequent generation of the equilibrium model. The algorithm relies on a topological diagram on top of the metric form and force diagrams known from graphic statics. This topological diagram supports a visual-oriented control of the qualitative load-bearing behaviour (i.e. connectivity and combination of inner force states) of discrete equilibrium models beyond conventional typological bounds. The CEM framework covers the initialization, the evaluation and the transformation of these equilibrium models in the light of the topological as well as the metric dimensions. In the transformation step, existing optimization algorithms can be additionally utilized to address constraints in both the form and the force domains. Design experiments highlight that these operations can be executed in many different ways and that the CEM framework can be used in both a bottom-up and in a top-down design mode. The real-time applicability of the developed framework is enabled by a computational implementation of the CEM algorithm into a digital toolkit. Depending on the context, the generated equilibrium models can be the ideal base for the conception of form-active, vector-active or section-active structures. The potential of the proposed framework is demonstrated through a series of case studies for bridges, multi-story buildings and stadiums.
last modified 6.5.2021